Published on

ES6) 함수형 프로그래밍을 위한 Lambda, Closure, Recursion

Authors
  • avatar
    Name
    Hoehyeon Jung
    Twitter

Functions

객체지향 프로그래미에서는 class를 기반으로 상속을 통한 재사용성을 높인다. 함수형 프로그래밍에서는 함수를 재사용 가능한 단위로 두고 이러한 함수를 합성하는 방식을 통해 재사용성을 높힌다.

함수를 재사용 가능한 가장 작은 단위로 두고자 한다면 함수가 자바스크립트에서 어떻게 동작하는지, 이를 함수형으로 어떻게 적용하는지에 대해서 정확하게 이용해야 한다.

Lambda Expression

람다 표현식은 수학적 개념인 람다 대수(Lambda Calculus)를 프로그래밍 언어에 도입한 개념이다. 람다 대수에 대한 개념 중에서 람다 대수의 함수의 표현에 대한 3가지 요소를 가져오면 다음과 같다.

  • 함수는 반드시 이름을 가질 필요는 없다. (익명 함수)
  • 함수의 입력 변수도 이름을 가질 필요는 없다.
  • 두 개 이상의 입력을 받는 함수는 하나의 입력을 받아 또다른 함수를 출력하는 함수로 반환할 수 있다. (Currying)

위 3가지 모두 ES5에서도 구현 가능한 부분 이었지만, 람다 대수의 개념을 도입해서 ES6에 만들어진 것이 화살표 함수(Arrow Function)이다.

// ES5
var addES5 = function (a, b) { // 익명 함수, 입력 변수 이름도 고정되지 않음
  return a + b;
}

// ES6
const addES6 = (num1, num2) => num1 + num2;

이러한 람다 표현식은 함수를 간결하고 읽기 쉬우며 재사용성 높게 만들 수 있는 토대가 되었다.

Closure

MDN에선 Closure를 다음과 같이 정의하고 있다.

A closure is the combination of a function bundled together (enclosed) with references to its surrounding state (the lexical environment).

JS에서 closure는 lexical environment를 감싸는 함수를 의미한다는 뜻으로 함수가 선언되는 시점에서의 환경을 저장하는 것을 의미한다.

const greeting = (name) => {
  const hi = 'hi';
  return (name) => console.log(`${hi} ${name}`);
};

const greetName = greeting();
greetName('gonewbie');

위 예제를 살펴보면 greeting 함수를 선언할 때 console.log를 출력하는 함수를 반환하면서 상위의 hi 변수를 참조하여도 문제가 없는 이유가 Closure 특성 떄문이다. 또한 이러한 변수는 외부에서 접근이 불가능하다.

이러한 특성은 Module 패턴을 통해 전역 변수를 더럽히지 않고, 안전하게 함수를 쓸 수 있다. 또한 선언 당시 컨텍스트만 참조하는만큼 Factory Pattern을 통해 선언 당시 상태를 기반으로 생성이 가능한데, 외부 상태를 참조하지 않은 순수한 함수를 작성하는 것을 가능하게 한다.

const add = (num1) => {
  return (num2) => num1 + num2;
}

const add5 = add(5);
const result = add5(10);
console.log(result); // 15

add 함수를 살펴보면 add 함수는 선언되는 시점에서 num2변수는 묶인 변수(Bound Variable)이 되어 있지만, num1의 경우는 어떻게 참조되는지 묶어있지 않은 자유 변수(Free Variable)이다. 람다 표현식(lambda expressions)에서 모든 variable이 묶인 변수일 경우엔 닫힌 표현식(Closed Expressions), 자유 변수가 하나 이상 있는 경우 열린 표현식(Open Expressions)라 한다.

이러한 자유 변수를 묶어주는 역할을 closure가 하는 것이다. 그 이름의 유래 역시 람다 표현식에서 열린 변수를 닫힌 변수로 만드는 것이기 때문에 선언 당시의 실행 컨텍스트를 포함해서 반환하는 것이다.

Currying

currying이란 람다 표현식에서 봤던 내용을 상기시켜보면, 함수가 받는 매개변수를 하나의 입력을 받아 또다른 함수를 호출하는 것이다. 이러한 Currying의 특성을 이용하면 함수를 재사용 가능성을 높이게 된다.

const pipe = (...funcs) =>
  (initValue) =>
    funcs.reduce((acc, func) => func(acc), initValue);

const evenDoubledreduce = pipe(
  x => x.filter(el => el % 2 === 0),
  x => x.map(el => el * 2),
  x => x.reduce((acc, cur) => acc + cur, 0)
)

const res = evenDoubledreduce([1,2,3,4,5,6]);

지난번에 언급한 적 있는 pipe 함수 역시 Currying을 이용하여서 구현되었다. pipe 함수를 이용해서 함수를 합성하면 합수를 합성한 함수를 반환할 뿐 결과를 출력하지 않는다. 이러한 현상은 closure의 경우처럼 함수를 선언한다고 해서 해당 함수를 실행한 결과를 저장하는 것이 아니라 함수 선언 당시 상황만을 저장한 것이다. Currying이나 Closure는 선언 당시 상황만 저장하기 떄문에 지연 평가(lazy evaluation)가 가능하다는 점과 선언 상황만을 저장하여 순수하게 함수를 합성하는 것이 가능해진다.

Recursive Function

함수형 프로그래밍에서는 loop를 다루는데 있어서 for, while과 같은 명령형으로 선언된 부분을 추상화거나 명령형으로 선언된 loop를 추상화하고 선언적인 함수를 통해 처리하는 방향으로 문제를 해결한다.

// imperative
const fibonacci = (number) => {
  const arr = [0, 1];
  for(let i = 2; i < number + 1; i++) {
    arr.push(arr[i-2] + arr[i-1]);
  }
  return arr[number];
}

// recursive (declarative)
const fibonacciR = (number) => {
  if (number < 2) return number;
  return fibonacciR(number - 1) + fibonacciR(number - 2);
}

위의 예제를 살펴보면 fibonacci 함수를 풀어내는데 있어 명령적인(imperative) 방법과 선언적인(declarative) 방법 두 가지 방법이 있다. 함수형 프로그래밍에서는 이러한 loop를 재귀적인(recursive) 방법, 즉 자기 자신을 호출하는 방식으로 문제를 쪼개서 해결한다. 프로그래밍적 문제 해결 방식 중 하나인 Divide and Conquer방식을 따라간 재귀적인 방식이 최선이라고 생각할 수 있다.

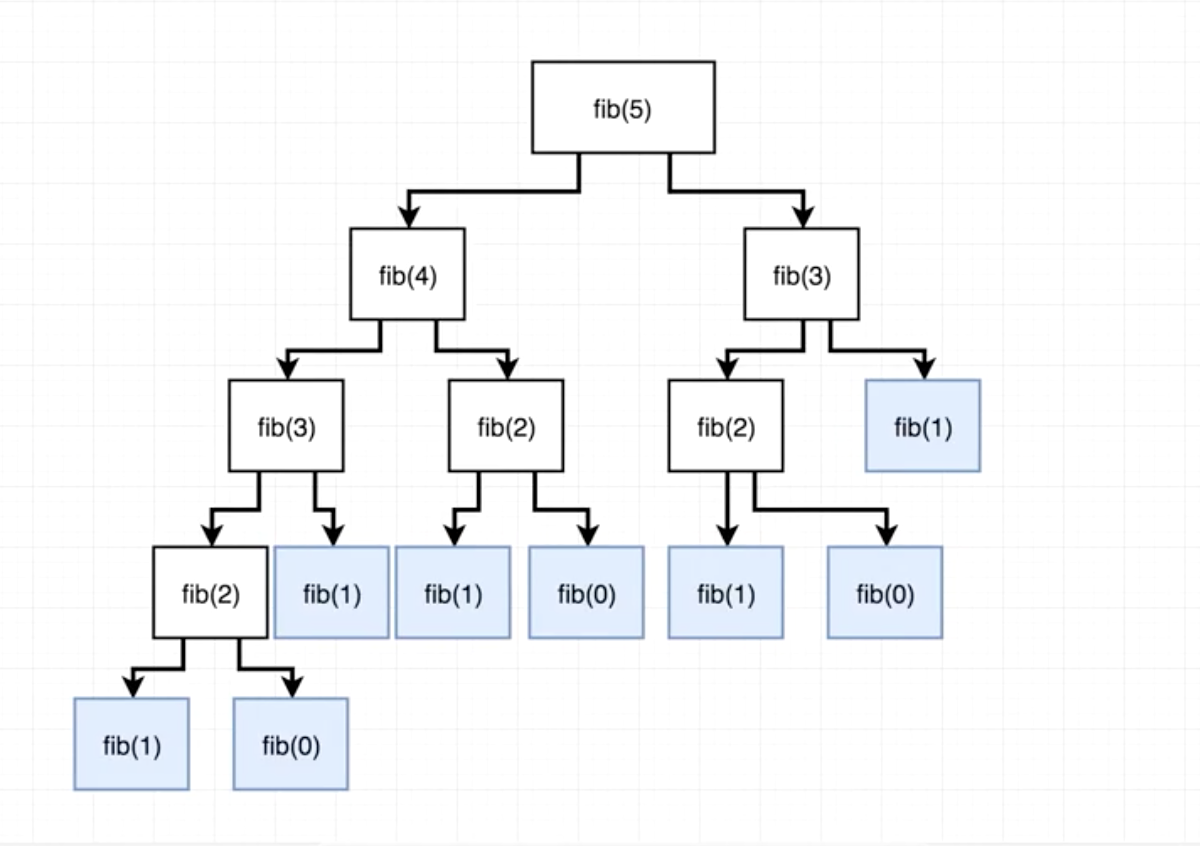
Fibonacci solution Recursively

Diagram from Stephen Grider’s “The Coding Interview Bootcamp“ course on Udemy.com

하지만 재귀함수를 다루는데 있어서 주의할 점이 존재한다. 함수를 호출하면 더 작은 함수를 호출하는 방식으로 문제를 나눠 해결하게 되는데 문제는 위의 해결 방식은 시간 복잡도가 O(2^n)에 해당되는 복잡한 해결방식이다.

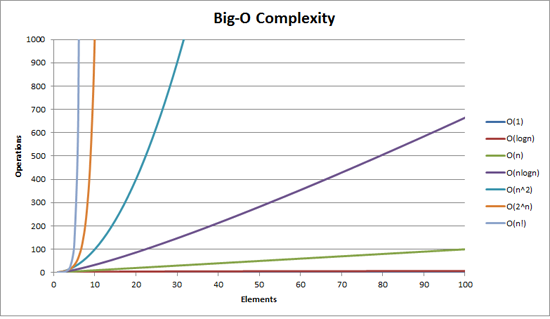
Big O Complexity

Memoization

시간복잡도 표를 보면 element 수가 늘어날수록 기하급수적으로(exponential)하게 증가하기 때문에 좋은 해결 방법은 아니다. 그럼, 재귀적으로 문제를 해결함에 있어 반복되는 문제를 해결할 수 없을까?

있다! 바로 memoization을 이용하는 것이다. 즉, 이전에 수행했던 계산을 저장하여 반복계산을 수행하는 것을 방지하는 것으로 문제를 해결할 수 있다.

const fibonacciR_Memo = (number, memo) => {
  memo = memo || {};
  if (memo[number]) return memo[number];
  if (number < 2) return number;
  return fibonacciR_Memo(number - 1, memo) + fibonacciR_Memo(number - 2, memo);
}

Memoization을 사용하면 이전에 수행된 데이터를 수행하기 때문에 시간 복잡도는 O(2n)으로 지수적인 증가가 선형적으로 바뀌어 속도가 훨씬 빨라지게 되었다!

Tail Call Optimization

재귀 함수를 호출하는데 있어서 또 다른 문제는 콜 스택을 초과하는 수행 등이 발생할 경우 처리가 불가능해진다. 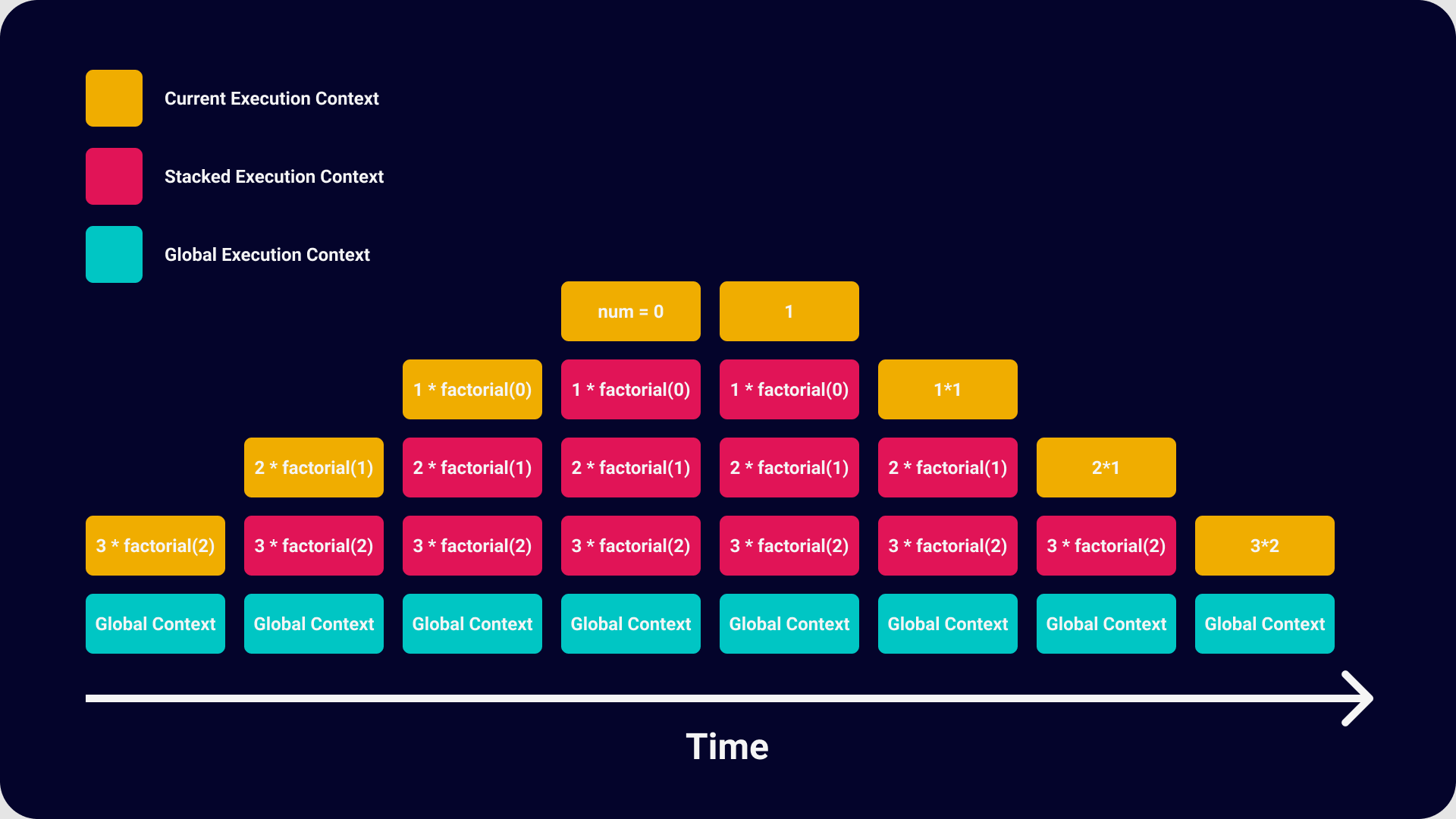Call Stack Changes in time

Image from https://medium.com/openmindonline/js-monday-06-adopting-memory-safe-recursion-d26dcee409c9

콜 스택에는 첫 실행 시 Global Context가 쌓이고 이후 함수들이 쌓이게 된다. 하지만 재귀 함수의 경우, 자기 자신을 호출하게 되는데, 이것이 call stack을 초과할 경우 문제가 발생하게 된다.

Max call stack size exceeded

그럼 메모리를 효율적으로 사용하지 못해서 콜 스택을 초과하는 문제에 대해서는 어떻게 해결해야 할까? ES6 Spec에는 존재하는 꼬리 재귀 최적화(Tail Call Optimization)을 통해 문제를 해결할 수 있다.

const fibonacciTCO = (n, sum = 0, prev = 1) => {
  console.log(sum, prev);
  return n <= 1 ? sum : fibonacciTCO(n - 1, prev + sum, sum);
}

TCO를 적용하기 위해서는 return에서 연산자를 사용하지 않아야 하며 호출될 함수를 포함해야 한다. 위의 예를 살펴보면 TCO를 통해 자기 자신을 호출하더라도 이는 콜스택에 쌓이지 않고 처리된다.

하지만 실제 브라우저에서 TCO 적용 여부를 살펴보면 Safari나 iOS Mobile만 지원하고 있어 적용 비율이 낮음을 알 수 있다. 링크 하지만 재귀함수를 다루는데 있어서 추후에 지원될 수 있는 TCO를 통한 최적화 수단을 아는 것이 중요하다 생각해 언급해보았다.

마치며

함수형 프로그래밍을 사용하는데 있어서 근간을 이루는 Closure, Currying, Recursion에 대하여 간략하게 알아보았다. 해당 개념들은 자바스크립트에서 함수가 어떻게 동작하는지에 대해서도 중요하지만 이러한 개념을 잘 녹여낸다면 함수형 프로그래밍에도 이를 적용할 수 있을 것이다.

참조

Discuss on Twitter • View on GitHub